Mérnök ember vagyok, így szeretem a precizitást, de be kell vallanom, hogy nem a műszaki egyetemen tanultam meg az ellenőrzés lapjait, hanem még a gimnáziumban geometria órán. Mielőtt azt gondolnád, hogy műszakin oktatják az ellenőrzést, el kell szomorítsalak, hogy a minőségbiztosítási szak kivételével komolyan nem oktatják. Mindenesetre én nem emlékszem rá, hogy nekem tanították volna.
Alapok
Ha az ellenőrzés témáját felvetem, bárhol akkor mindenki azt mondja, hogy persze szoktunk ellenőrizni, de a valóság az, hogy ha ellenőriznek is akkor lehető legkevésbé hatékony helyen azaz a folyamat végén vagy egyáltalán nem ellenőrzik a tevékenységeket.
Miért van ez?
Azért mert ha felmerül egy probléma vagy kapunk egy új feladatot amire az eddig alkalmazott mechanizmusuk nem alkalmazhatóak akkor keresni kell egy új megoldást. Keressük és megtaláljuk. Örülünk és elkezdünk ennek mentén dolgozni. Itt jön az általam egyébként annyira kedvelt és sokat használt „80-20”.
Amikor megtaláljuk a megoldást, és bár jól meggondoltuk és általános megoldásnak látszik, de valójában csak 80%-ban fedi az igényeket, csak ezt akkor még nem látjuk. A problémák később jelentkeznek használat közben. Miért? Mert nem ellenőriztük a szélsőértékeket, nem végeztünk próbákat és nem teszteltünk mielőtt bevezettük a módosítást.
A szélsőérték vizsgálat a diszkusszió egyik lényeg. De a legfontosabb az, hogy gondoljunk rá hogy mi van a nem általános esetben, és legalább egyszer próbáljuk ki, hogy tényleg működik-e a rendszer valós környezetben is. Ez még nem tesztelés ez csak egy egyszerű próba. A tesztelés megint csak megér egy misét, elöljáróba csak annyit:
- egy mérés nem mérés
- két mérés nem mérés
- három mérés egy mérés
- minimum 3 mérés kell, hogy a mérési hibák kiküszöböld (azaz 9 et kell mérni)
Hogy csináld a diszkussziót és mi az a szélsőérték vizsgálat.
Sajnálom, de ez matematika. Sokféleképpen lehet magyarázni de hogy szemléletes legyen én a két körhöz érintő egyenes illesztésével mutatnám be.
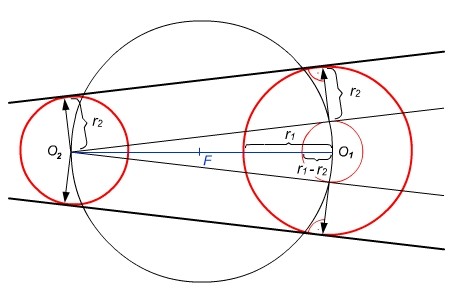
A szerkesztés első lépése így hangzik:
1. 1. Vegyél fel a síkon egy R1 és egy R2 sugarú kört
2. …..
A többivel nem fárasztok senkit, de nézzük át ennek a pontnak a diszkusszióját.
1. mi van akkor ha a R1=R2 ez biztos speciális eset lesz
2. sőt mi van akkor ha koncentrikus köröket veszünk fel?
· Ebben az esetben NEM lehet érintő egyenest szerkeszteni.
A példából számomra remekül látszik, hogy azért,mert egy problémára végtelen számú megoldás van ugyan úgy lehet végtelen számú kivétel is . Szóval érdemes végiggondolni a diszkussziót.
A gyakorlatban
Lefordítva egy kicsit ezt az elméleti eszmefuttatást egy egyszerű esetre. Keressünk szélsőértékeket egy rendezvény szervezésénél. Elsőre hülyeségnek tűnhet, de nem az:
Meghívtunk 100 embert, azt várjuk hogy 25 eljön az eseményre. Ez egy realisztikus várakozás, lehet azt mondani, hogy pesszimista, de nézzük meg a szélsőértékeket:
1. Nem jön el senki – le kell mondani!
a. ha 3 nappal előtte nincs még regisztráció akkor lemondjuk
b. Ki mondja le? Milyen formában? stb.
2. Eljön mind a 100 ember (vagy több mert mindenki hozott még egy embert)
a. 3 nappal előtte helyszínt kell változatni
b. Értesíteni kell a résztvevőket…stb
A szélsőérték vizsgálatban nem azt vizsgáljuk, hogy mennyi az esély ennek, hanem hogy van-e megoldás arra az esetre. A geometriai példa is mutatta, hogy a szélső értékeken van olyan eset ami speciális de ad megoldást és van amikor egyszerűen nincs megoldás.
Ha egy nappal a meghirdetett dátum előtt rendezvény felkerül a facebookra és 1000 ember jelenik meg akkor arra szerintem nincs épeszű megoldás.
Rizikó – vagy megoldás
Általában azt a megoldást találjuk meg először ami a leggyakoribb megoldást adja, majd a diszkusszió során végignézzük azokat az eseteket amikor működik, de speciális és azokat ahol nincs megoldás, nincs más hátra mint megbecsüljük a számosságukat.
Ilyenkor kiderül, hogy az általunk elsőre megtalált megoldás mennyire általános. Ha azt látjuk hogy a speciális esetek száma kevés és kezelhetőek. Akkor minden rendben nem fog meglepetés érni bennünket a használat közben.
Ha ennyit sem teszünk meg akkor szerintem igen sok meglepetés fog majd érni. De ha esetleg kételkedsz, hogy megtaláltál-e minden speciális esetet akkor csak kérdezz meg.






